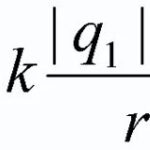전위의 개념은 정전기 및 전기 역학 이론의 중요한 기초 중 하나입니다. 그 본질을 이해하는 것은 이러한 물리학 분야에 대한 추가 연구를 위한 필수 조건입니다.
전위란 무엇인가
고정 전하 Q에 의해 생성된 필드에 단위 전하 q를 놓으십시오. 쿨롱 힘 F=k*Qq/r.
여기 아래 k=((1/4)*π* ε* ε), 여기서 ε0 — 전기 상수(8.85*10-12 F/m), ε은 중간 유전 상수.
기여 요금 이 힘의 작용으로 움직일 수 있고 힘은 일정량의 일을 할 것입니다. 이것은 두 전하의 시스템이 두 전하의 크기와 전하 사이의 거리에 따라 달라지는 위치 에너지를 가지며 이 위치 에너지의 크기는 전하 q의 크기에 의존하지 않는다는 것을 의미합니다. 여기에 전위의 정의가 도입되었습니다. 이것은 전하의 크기에 대한 필드의 위치 에너지의 비율과 같습니다.
φ=W/q,
여기서 W는 전하 시스템에 의해 생성된 필드의 위치 에너지이고, 퍼텐셜은 필드의 에너지 특성입니다. 전기장에서 전하 q를 일정 거리 이동하려면 쿨롱 힘을 극복하기 위해 일정량의 일을 해야 합니다. 한 점의 포텐셜은 이 점에서 무한대로 단위 전하를 이동시키는 데 소비되어야 하는 일과 같습니다. 이때 다음 사항에 유의해야 합니다.
- 이 일은 전하의 위치 에너지의 감소와 같을 것입니다(A=W2-W1);
- 작업은 요금의 궤적에 의존하지 않습니다.
SI 시스템에서 전위의 단위는 1볼트입니다(러시아 문헌에서는 V로 표시되고 외국 문헌에서는 V로 표시됨). 1V \u003d 1J / 1C, 즉 1C의 전하를 무한대로 옮기는 데 1줄이 걸린다면 1볼트 지점의 전위에 대해 이야기할 수 있습니다. 이름은 전기 공학의 발전에 크게 기여한 이탈리아 물리학자 알레산드로 볼타를 기리기 위해 선택되었습니다.
전위가 무엇인지 시각화하기 위해 두 물체의 온도 또는 공간의 다른 지점에서 측정된 온도와 비교할 수 있습니다. 온도는 물체의 가열을 측정하고 전위는 전하를 측정합니다. 한 몸이 다른 몸보다 더 뜨겁다고 말하며, 한 몸은 더 많이 충전되고 다른 몸은 덜 충전된다고 말할 수도 있습니다. 이 몸은 다른 잠재력을 가지고 있습니다.
전위 값은 좌표계의 선택에 따라 달라지므로 어느 정도 수준이 필요하며 이 값은 0으로 간주해야 합니다. 예를 들어 온도를 측정할 때 녹는 얼음의 온도를 기준으로 삼을 수 있습니다.전위의 경우 무한히 먼 지점의 전위는 일반적으로 0 레벨로 간주되지만 일부 문제, 예를 들어 접지 전위 또는 커패시터 플레이트 중 하나의 전위를 해결하기 위해 0으로 간주할 수 있습니다.
잠재적 속성
잠재력의 중요한 속성 중 다음 사항에 유의해야 합니다.
- 필드가 여러 전하에 의해 생성되면 특정 지점의 전위는 각 전하 φ=φ에 의해 생성된 전위의 대수적(전하 부호 고려) 합계와 같습니다.1+φ2+φ3+φ4+φ5+…+φN;
- 전하로부터의 거리가 전하 자체를 점 전하로 간주할 수 있는 거리인 경우 총 전위는 공식 φ=k*(q1/아르 자형1+q2/아르 자형2+q3/아르 자형3+…+qN/아르 자형N), 여기서 r은 해당 전하로부터 고려된 점까지의 거리입니다.
필드가 전기 쌍극자(반대 부호의 연결된 두 전하)에 의해 형성되면 쌍극자로부터 거리 r에 위치한 임의의 지점에서의 전위는 φ=k*p*cosά/r과 같습니다.2, 어디:
- p는 쌍극자의 전기 암으로 q*l과 같습니다. 여기서 l은 전하 사이의 거리입니다.
- r은 쌍극자까지의 거리입니다.
- ά는 쌍극자 암과 반경 벡터 r 사이의 각도입니다.
점이 쌍극자의 축에 있으면 cosά=1이고 φ=k*p/r입니다.2.
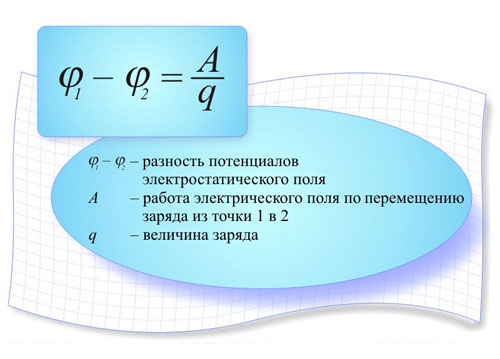
잠재적 차이
두 점에 일정한 전위가 있고 같지 않으면 두 점 사이에 전위차가 있다고 말합니다. 다음과 같은 점 사이에 전위차가 발생합니다.
- 그의 잠재력은 다른 징후의 요금에 의해 결정됩니다.
- 임의의 부호 전하로부터 전위가 있는 점과 전위가 0인 점;
- 같은 부호의 전위를 가지지만 절대값이 다른 점.
즉, 전위차는 좌표계의 선택에 의존하지 않습니다.0 표시(예: 해수면)를 기준으로 서로 다른 높이에 위치한 물웅덩이에 비유할 수 있습니다.
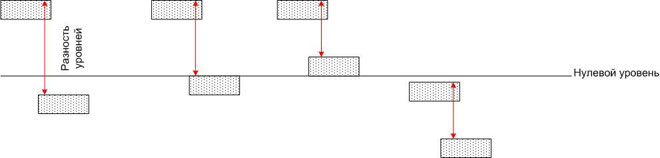
각 풀의 물에는 특정 위치 에너지가 있지만 두 개의 풀을 튜브로 연결하면 각각에 물의 흐름이 있으며 그 유량은 튜브의 크기뿐만 아니라 , 그러나 또한 지구 중력장의 잠재적 에너지의 차이(즉, 높이 차이). 이 경우 잠재적 에너지의 절대값은 중요하지 않습니다.
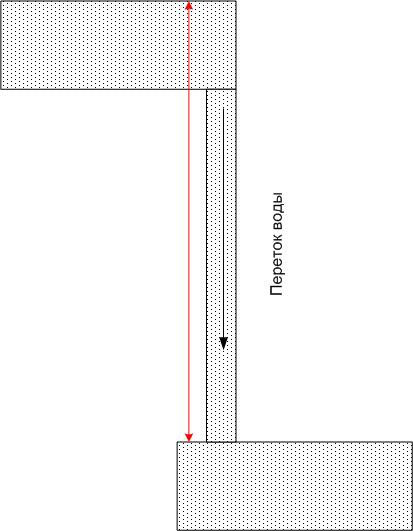
마찬가지로 전위가 다른 두 점을 도체로 연결하면 전류가 흐르게 됩니다. 전기, 도체의 저항뿐만 아니라 전위차(절대값이 아님)에 의해 결정됩니다. 물에 대한 비유를 계속하면 위쪽 웅덩이의 물이 곧 고갈되고 물을 다시 위로 이동시키는 힘(예: 펌프)이 없으면 흐름이 매우 빠르게 멈춘다고 말할 수 있습니다.
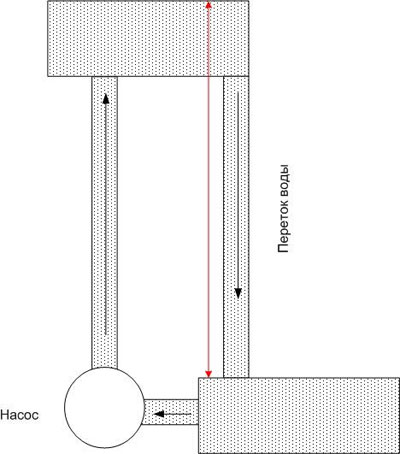
따라서 전기 회로에 있습니다. 특정 수준의 전위차를 유지하려면 가장 높은 전위를 가진 지점으로 전하(더 정확하게는 전하 캐리어)를 전달하는 힘이 필요합니다. 이 힘을 기전력이라고 하며 EMF로 약칭합니다. EMF는 전기 화학적, 전자기 등 다른 성질을 가질 수 있습니다.
실제로, 중요한 것은 주로 전하 캐리어 궤적의 초기 지점과 최종 지점 간의 전위차입니다. 이 경우 이 차이를 전압이라고 하며 SI에서는 볼트로도 측정됩니다.한 지점에서 다른 지점으로 1쿨롱의 전하를 이동할 때 필드가 1줄의 작업을 수행하는 경우 1볼트의 전압에 대해 이야기할 수 있습니다. 즉, 1V \u003d 1J / 1C이고 J / C도 잠재적인 차이.
등전위 표면
여러 점의 전위가 같고 이러한 점이 표면을 형성하는 경우 이러한 표면을 등전위라고 합니다. 이러한 속성은 예를 들어 전하 주위에 구를 둘러싸고 있습니다. 그 이유는 전계가 모든 방향에서 거리에 따라 동일하게 감소하기 때문입니다.
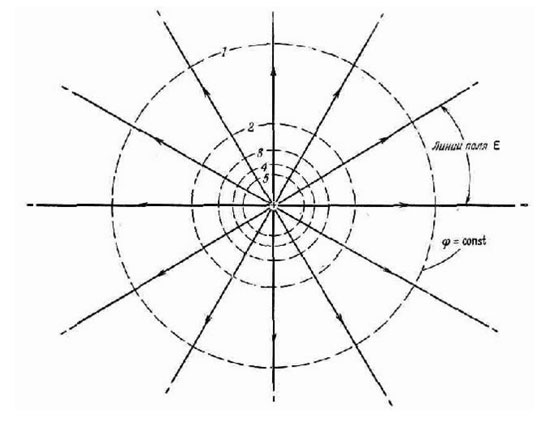
이 표면의 모든 점은 동일한 위치 에너지를 가지므로 그러한 구체 위로 전하를 이동할 때 일이 소모되지 않습니다. 여러 전하의 시스템의 등전위 표면은 더 복잡한 모양을 갖지만 한 가지 흥미로운 속성이 있습니다. 즉, 절대 교차하지 않습니다. 전기장의 힘선은 각 점에서 동일한 전위를 갖는 표면에 항상 수직입니다. 등전위면을 평면으로 자르면 등전위선이 얻어집니다. 등전위면과 동일한 특성을 가지고 있습니다. 예를 들어, 실제로 정전기장에 놓인 도체 표면의 점은 동일한 전위를 갖습니다.
전위와 전위차의 개념을 다루었으므로 전기 현상에 대한 추가 연구를 진행할 수 있습니다. 그러나 더 일찍이 아닙니다. 기본 원리와 개념을 이해하지 않고 지식을 심화할 수 없기 때문입니다.
유사한 기사: